Le Challenge FHCP
Le 30 septembre 2015, l'équipe de recherche en Théorie des Graphes de la Flinders University d'Adelaïde (Australie) donnait le départ d'un concours ouvert à tous sur le globe.
Elle mettait à disposition de chercheurs, d'ingénieurs et de tout les curieux une collection de 1001 graphes (i.e. des réseaux de points connectés entre eux), et demandait aux participants de démontrer l'existence, dans chacun de ces graphes, d'un circuit passant par les arêtes de ce graphe et visitant une fois et une seule tous ses sommets.
L'objectif des organisateurs était de faire un "état de l'art" des méthodes connues par les scientifiques et de mesurer leur efficacité en pratique. Le concours devait également permettre d'identifer les graphes vraiment difficiles, c'est-à-dire ceux que personne n'arriverai à résoudre. Nous étions de notre côté curieux de découvrir si le savoir et les programmes que nous avions accumulés par le passé nous permettraient d'aller très loin, et si participer à ce concours nous amènerait à les améliorer encore. Nous avons remporté ce concours en résolvant 985 graphes.
Les cycles d'un graphe passant une fois et une seule par chaque sommets sont connus dans la littérature scientifique sous le nom de Cycles Hamiltoniens. C'est un cas particulier du problème du Voyageur de Commerce, sur lequel ce magazine a déjà publié un article. Ce problème a été défini en 1857 par William Rowan Hamilton, un scientifique irlandais, et avait déjà été étudié en 1856 par Thomas Penyngton Kirkman. C'est depuis un problème très étudié en théorie des graphes.
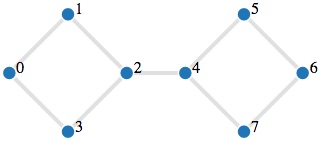
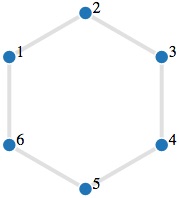
Le graphe suivant contient un tel cycle: pouvez-vous le trouver en cliquant sur ses liens ? Plusieurs solutions existent.
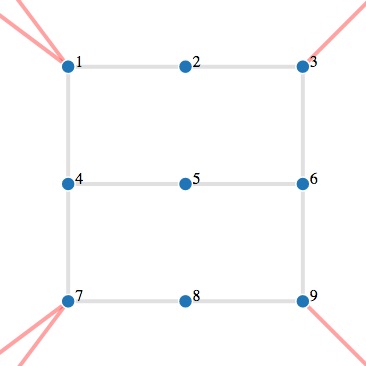
Les deux graphes suivants ne sont pas hamiltoniens. Pour le graphe de gauche, l'arête entre les sommets 2 et 4 sépare le graphe en deux parties. Or, pour trouver un cycle hamiltonien, il faut pouvoir aller au moins une fois de la partie gauche vers la partie droite, puis revenir de la partie droite vers la partie gauche. Comme il n'y a qu'une seule arête entre les deux parties, ce n'est pas possible. Une telle arête est appelée un pont, et tout graphe contenant un pont n'est pas hamiltonien.
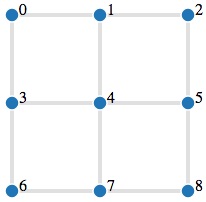
Il est un peu plus difficile de comprendre pourquoi le graphe de droite (la grille) n'est pas hamiltonien. Pour cela, il faut d'abord observer que ce graphe est biparti, c'est-à-dire que l'on peut séparer ses sommets en un ensemble $I$ (les sommets impairs) et un ensemble $P$ (les sommets pairs) et observer que chaque sommet de $I$ n'est relié qu'à des sommets de $P$ (et réciproquement). S'il existait un cycle hamiltonien, alors ce cycle passerait par le sommet 0 (qui est pair) puis sur un sommet impair, puis sur un sommet pair, et ainsi de suite en alternant. Le graphe contenant 9 sommets en tout, le dernier sommet découvert par le cycle avant de revenir au sommet 0 sera nécessairement un sommet pair. Mais c'est totalement impossible, puisque 0 ne peut pas être relié à un sommet pair !
Le problème du Cycle Hamiltonien est ce qu'on appelle un problème de décision. Il s'agit de décider si il est vrai ou faux que le graphe contient un cycle passant une et une seule fois par chacun de ces sommets. Le problème du voyageur de commerce est quant à lui un problème d'optimisation. En effet, il s'agit de trouver le cycle le plus court passant au moins une fois par chacun des sommets.
Règlement du concours
Il suffisait pour remporter ce concours, et le prix de 1001USD, d'être le premier à résoudre le problème du Cycle Hamiltonien pour chacun des 1001 graphes. Si personne n'en était capable, la victoire irait à celui qui en aurait résolu le plus grand nombre un an plus tard.
Toutes les méthodes imaginables étaient autorisées pour participer à ce concours. En particulier, il n'était pas interdit de résoudre le problème ... à la main ! Mais la taille des graphes allant de 66 sommets (le plus petit) à 9528 sommets (le plus gros), il était plus raisonnable de le faire par ordinateur.
L'oracle
Dans cet article, nous utilisons le terme "oracle" pour désigner un programme informatique qui, étant donné un graphe, répond "VRAI" si il a trouvé un cycle hamiltonien (qu'il retourne également) ou "FAUX" si il a prouvé que le graphe n'est pas hamiltonien (i.e., il ne contient pas de cycle hamiltonien).
En pratique, l'oracle est l'implémentation d'une des nombreuses méthodes qui ont été proposées par les scientifiques pour résoudre le problème du cycle hamiltonien. Dans ces méthodes, on trouve des algorithmes dédiés à des graphes ayant une propriété spécifique (par exemple la propriété: "tous les sommets ont degré 3"). Ces algorithmes nécessitent de savoir détecter si le graphe possède réellement cette propriété, ce qui est parfois difficile à tester. D'autres algorithmes utilisent des méthodes générales comme la programmation dynamique, le principe de la procédure de séparation et évaluation, ou encore la programmation linéaire. Nous avons choisi d'utiliser une méthode basée sur la programmation linéaire en nombres entiers (voir l'annexe Formulation pour plus de détails sur cette méthode). Cette méthode offre de bonnes performances en général même si elle peut échouer sur des petits graphes.
La table suivante montre le temps de calcul nécessaire à notre oracle pour trouver la solution des premiers graphes. Nous observons des temps de calculs très variables ou des graphes plus gros peuvent être résolus beaucoup plus vite que des graphes plus petits. Nous observons surtout des temps de calculs très importants comme pour le graphe n°12. Le problème du cycle hamiltonien étant difficile à résoudre, il n'est pas surprenant que le temps mis par l'oracle pour retourner sa réponse puisse être très long (des années). Sachant que les graphes ont en moyenne 3000 sommets, l'utilisation seule de l'oracle n'aurait pas suffit. Notons tout de même que, à notre grande surprise, l'oracle a trouvé en 5 minutes la solution du graphe n°1000 qui a pourtant 9058 sommets.
| n° | Nombre de sommets | Temps (en secondes) |
|---|---|---|
| 1 | 66 | 0.76 |
| 2 | 70 | 0.01 |
| 3 | 78 | 0.06 |
| 4 | 84 | 10.85 |
| 5 | 90 | 33.20 |
| 6 | 94 | 0.66 |
| 7 | 102 | 42.00 |
| 8 | 108 | 1574.00 |
| 9 | 114 | 105.30 |
| 10 | 118 | 0.17 |
| 11 | 126 | 168.10 |
| 12 | 132 | 89631.00 |
| 13 | 138 | 240.00 |
| 14 | 142 | 16.00 |
Notre travail a consisté à développer des méthodes spécifiques pour aider l'oracle, en nous basant sur notre compréhension de la structure des graphes. Ces méthodes, que nous décrivons dans la suite, consistent par exemple à découper le problème en sous-problèmes plus petits (voir par exemple la section 2-connexité), à substituer des parties du graphe par des graphes plus simples (section motif de taille 16), à prouver que certaines arêtes peuvent être supprimées, ou encore à imposer un ensemble d'arêtes (l'oracle cherche alors si il existe un cycle hamiltonien contenant ces arêtes). Pour le graphe n°12, nos méthodes nous permettent maintenant d'obtenir la solution en moins d'une seconde.
Pour les simplifier il faut les comprendre. Quelle tête ont donc ces graphes?
A la découverte des graphes
Impossible de résoudre un tel problème sans avoir une représentation visuelle de ces graphes. Nous avons donc commencé à les visualiser un par un, et ce que nous avons découvert nous à beaucoup aidés. En cliquant sur les liens bleus à droite de l'écran, vous en verrez autant que nous.
Des presque-cycles
A notre grande surprise, beaucoup de graphes ressemblaient déjà à des cycles. Notre oracle aurait dû être capable de trouver un Cycle Hamiltonien tout seul, mais à y regarder de plus près le problème était plus compliqué.
En effet, chacun de ces cycles est en réalité composé de trois brins principaux, liés par un maillage. Il existe beaucoup de façons de faire passer un chemin hamiltonien à l'intérieur de tels maillages, et pour cette raison notre oracle avait du mal à se décider car il cherchait à les explorer toutes.
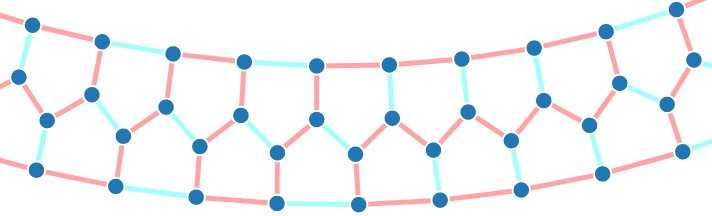
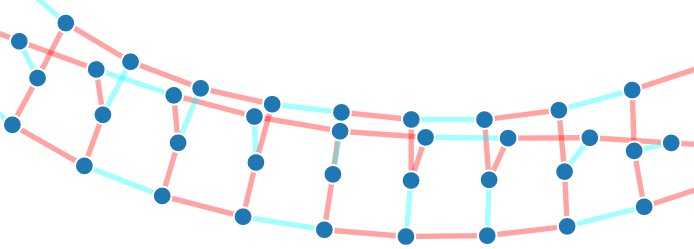
De plus, bien que ces graphes semblent n'être qu'un long enchainement du même motif, il existe dans chacun d'entre eux un point particulier autour duquel le maillage est légèrement différent: c'est là que notre oracle devrait concentrer ses efforts, au lieu d'hésiter sur le chemin à emprunter là ou le maillage est simple !
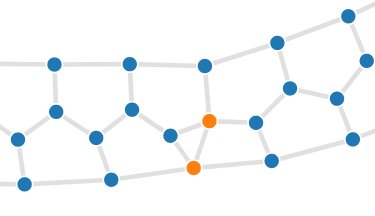
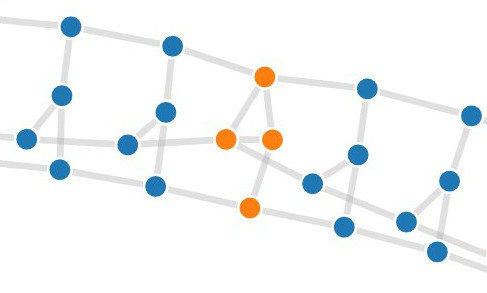
Pour aider notre algorithme, nous avons tout simplement retiré des arêtes (i.e. des liens) du graphe là où le maillage était simple, afin de ne plus laisser l'oracle hésiter inutilement: il lui restait à ces endroits si peu d'arêtes qu'il avait à peine de quoi faire passer un chemin ! En revanche, nous lui avons laissé faire la partie difficile du travail lorsque le maillage était plus compliqué.
Le problème des cloches
Les graphes de cette famille sont ceux qui ont su nous résister jusqu'à la fin.
Les plus petits exemples de cette famille présents parmi les 1001 graphes ont été résolus sans problème par notre oracle, mais ils sont rapidement devenus trop complexes. De plus, la visualisation de ces graphes ne nous apprend pas grand chose.

En revanche, ces graphes possèdent plusieurs symétries au sens de la théorie des groupes (cf. Wikipedia). Nous avons également réussi à décortiquer ces graphes jusqu'à nous rendre compte qu'ils étaient la superposition de centaines de copies de deux graphes très simples, représentés ci-dessous:
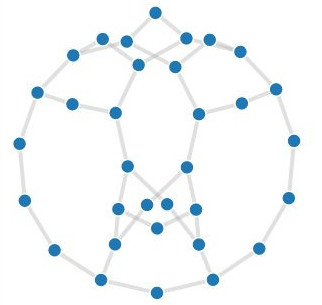
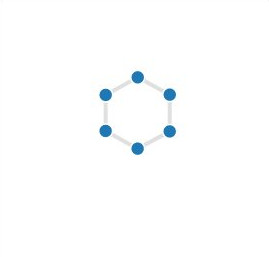
Malgré celà, et malgré bien d'autres observations faites par la suite, nous n'avons jamais réussi à exploiter leur structure au point de trouver un Cycle Hamiltonien dans chacun d'entre eux. D'où viennent-ils ? Nos différentes explorations nous avaient indiqué que la structure de ces graphes était très réfléchie.
La réponse à cette question nous a été apportée par les organisateurs après la fin du concours. Ces graphes trouvent leur origine dans le problème combinatoire de change ringing (cf. Wikipedia en version anglaise): il s'agit d'une façon de faire sonner à tour de roles les k cloches d'une église jusqu'à avoir entendu toutes les cloches dans tous les ordres possibles (i.e. toutes les permutations).
Plus précisément, imaginons que 5 cloches sont disposées en face de nous, et qu'a côté de chacune d'entre elle se trouve un sonneur. Les sonneurs sont identifiés par des numéros allant de 1 à 5, et sonnent chacun leur cloche quand c'est leur tour. Après que chaque sonneur ait sonné sa cloche, il a la permission d'aller vers une nouvelle cloche (mais attention, une cloche doit toujours avoir un sonneur !) et de recommencer ce processus.
Combien de fois est-il possible de répéter ce processus sans entendre deux fois la même mélodie ? La réponse est $5!=120$, car c'est le nombre total de mélodies possibles. Pour simplifier le travail des sonneurs, on leur a donné deux façons de se déplacer entre eux afin que les changements soient plus faciles à mémoriser, qui sont appelées les changements de Erin. Est-il toujours possible d'explorer les $5!$ possibilités en suivant uniquement les changements de Erin ? Si oui, est-il possible de les explorer toutes et de revenir finalement à la position de départ ?
Ce problème est difficile à résoudre, et les auteurs du concours l'avaient traduit en un graphe dont l'existence d'un cycle hamiltonien fournissait une solution au problème précédent. Mais nous étions très loin d'imaginer tout cela en analysant les propriétés du graphe !
Les auteurs du concours ont expliqué leur méthode dans un article de recherche disponible en ligne pour les lecteurs curieux d'en savoir plus.
Les 'BigDegree'
Ces graphes se distinguent des autres parce qu'ils ont deux sommets de très gros degré (deux sommets de degré 192 pour le graphe n°268 et les autres sommets ont degré au plus 6). Ici, l'affichage du graphe ne nous apporte aucune information exploitable.

Maintenant, si nous retirons les deux sommets de plus gros degré, alors une structure se dégage. C'est une sorte de double grille avec des motifs supplémentaires.

Si nous regardons d'encore plus près, nous pouvons voir que le graphe contient de multiples copies du sous-graphe suivant. Les sommets 1, 3, 7 et 9 sont reliés au reste du graphe par une ou deux arêtes. Ce sous-graphe a la particularité que si le cycle hamiltonien arrive par le sommet 1, alors il suivra obligatoirement et dans l'ordre les sommets 1, 2, 3, 6, 5, 4, 7, 8 puis 9 avant de ressortir. Si le cycle arrive par le sommet 3, alors il suivra dans l'ordre les sommets 3, 2, 1, 4, 5, 6, 9, 8, 7 avant de ressortir. Ceci nous indique que le graphe a une structure très forte et que peu de choix suffisent pour forcer un très grand nombre d'arêtes.
Pour trouver les cycles hamiltoniens dans ces graphes, nous avons d'abord remarqué que les sommets de gros degré ont un voisin de degré 2, ce qui permet de fixer une arête du cycle. Nous avons ensuite cherché la seconde arête incidente au sommet de plus gros degré par essai/erreur (voir degré 2), c'est à dire en imposant une arête avant d'interroger l'oracle. Celui-ci répond rapidement si ce choix conduit à une impossibilité, auquel cas l'arête est supprimée et on recommence avec une autre, ou si c'est le bon choix.
Le motif de taille 16
A force de visualiser des graphes en s'interrogeant sur leur structure, nous avons trouvé qu'un petit motif revenait régulièrement. Il n'avait pas l'air assez gros pour poser problème à notre oracle, mais il apparaissait très souvent et semblait avoir été placé là avec une intention très précise.
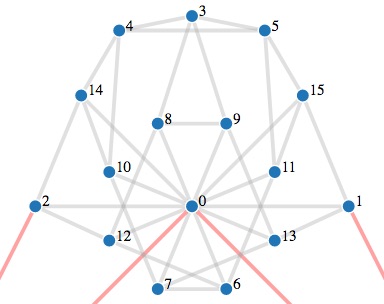
Ce motif possède 16 sommets, et n'est relié au reste du graphe que par quatre liens: deux liens sont rattachés au sommet central (0 sur la figure), et un lien vers le reste du graphe part de chacun des sommets 1 et 2 (qui ont exactement trois voisins sur la figure).
Quelles sont ses propriétés ? Comment un cycle hamiltonien peut-il passer à travers ce petit motif ? Puisque seuls trois sommets sont reliés au reste du graphe, il n'existe que quatre possibilités:
- Le cycle entre par 0, visite les 16 sommets et ressort par 1 (ou inversement).
- Le cycle entre par 0, visite les 16 sommets et ressort par 2 (ou inversement).
- Le cycle entre par 1, visite les 16 sommets et ressort par 2 (ou inversement).
- Le cycle entre par 0 et ressort immédiatement.
Plus tard, il rentrera par 1 et sortira par 2 après avoir visité les 15 sommets qui n'ont pas encore été vus (ou inversement).
Nous avons vérifié que toutes ces possibilités étaient réalisables, c'est-à-dire que les liens de ce petit motifs permettaient de trouver dans ces 16 sommets les chemins évoqués dans les 4 possibilités ci-dessus. Que pouvons-nous faire avec une telle information ?
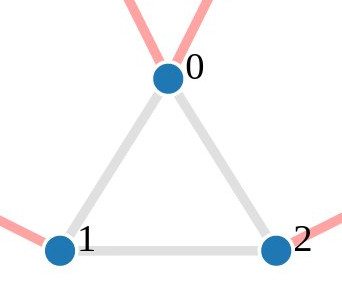
Nous pouvons nous rendre compte qu'il existe un graphe plus simple ayant la même propriété, et que ce graphe est un triangle. Il ne nous restait plus qu'à écrire un programme permettant de detecter automatiquement ce graphe à 16 sommets, et de le remplacer par un triangle pour simplifier le travail de notre oracle. En effet, le graphe n°48 qui a 338 sommets est transformé en un graphe à 78 sommets. Le graphe n°400 a 2366 sommets est transformé en un graphe à 546 sommets. D'autres techniques peuvent ensuite être appliquées pour réduire encore la taille du graphe, comme la décomposition en composantes 3-sommet-connexe. Une fois le problème résolu avec ces triangles, on pouvait facilement reconstruire la solution du problème original en analysant, pour chaque motif, les 4 possibilités.
La race du 1001
Le graphe ayant le numéro 1001 a 9528 sommets. Il est beaucoup trop complexe pour notre oracle, mais possède une structure qui nous permet de le décomposer en petites parties. Bien entendu, la visualisation est assez longue et il est nécessaire de déplacer certains sommets manuellement pour y comprendre quelque-chose.
Avec un peu de volonté on arrive au résultat suivant :

On remarque aisément la présence d'une petite trentaine de gros 'blocs' denses, liés aux autres par un nombre très réduit de liens. Nous aimerions assez pouvoir découper ce graphe en séparant les blocs les uns des autres, mais il faut pour cela comprendre la structure des liens qui les lient.
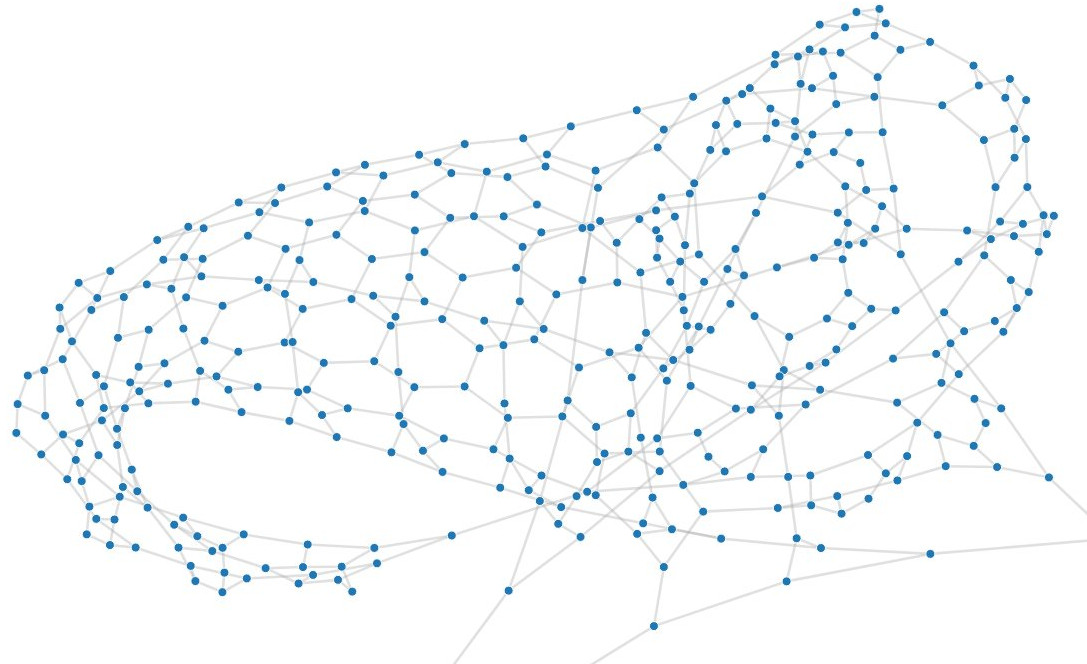
Fort heureusement, les liens entre ces blocs et le reste du graphe ne passent que par 4 sommets (voir image ci-dessus) : nous pouvons utiliser cette information pour simplifier le calcul d'un cycle Hamiltonien.
En effet, comme pour le motif de taille 16 présenté plus haut, il n'est pas nécessaire de savoir où exactement passe le chemin hamiltonien à l'intérieur d'un bloc donné pour savoir où il doit passer dans les autres blocs: il suffit de savoir en quels points du bloc le cycle hamiltonien rentre, en quels points il ressorts, et peu importe ce qu'il fait au milieu de son parcours à l'intérieur du bloc !
Puisque seuls 4 sommets connectent chaque bloc au reste du graphe, il n'existe que très peu de possibilités (au maximum 9), et chaque bloc est suffisemment petit pour qu'il soit possible de calculer cette information.
Composition de graphes
La 2-connexité
Un graphe est dit connexe si il est possible de relier toute paire de sommets par un chemin. Un graphe est 2-sommets-connexe si il reste connexe après la suppression de n'importe quel sommet, il est 3-sommets-connexe si il reste connexe après la suppression de n'importe quelle paire de sommets, et ainsi de suite.
Une condition nécessaire à l'existence d'un cycle hamiltonien est que le graphe soit 2-sommets-connexe. Il est en effet facile de voir que si le graphe n'est pas 2-sommets-connexe, alors il existe un sommet s dont la suppression sépare le graphe en 2 sous-graphes A et B (i.e., A et B n'ont ni sommet commun ni arête de l'un vers l'autre), ce qui revient à dire que tout chemin d'un sommet de A vers un sommet de B passe par s. Comme un cycle hamiltonien passe une seule fois par un sommet, une fois arrivé dans B, on ne peut plus revenir dans A pour fermer le cycle.

Maintenant, supposons qu'il existe 2 sommets u et v qui séparent le graphe en 2 sous-graphes A et B (i.e., dont la suppression découpe le graphe en 2 sous-graphes). Alors, un cycle hamiltonien dans le graphe est l'union d'un chemin hamiltonien de u à v n'impruntant que les sommets de A et d'un chemin de v à u n'empruntant que les sommets de B.
Cette propriété est très intéressante car elle permet de découper un graphe en un ensemble de graphes plus petits. En effet, nous pouvons construire 2 graphes, le premier contenant A, les sommets u et v et les arêtes les reliant à A, plus un nouveau sommet z relié à u et v. Le deuxième graphe est construit de la même façon avec B. Il reste à trouver un cycle hamiltonien dans chacun de ces graphes que nous pourrons ensuite assembler pour obtenir un cycle hamiltonien dans le graphe d'origine.
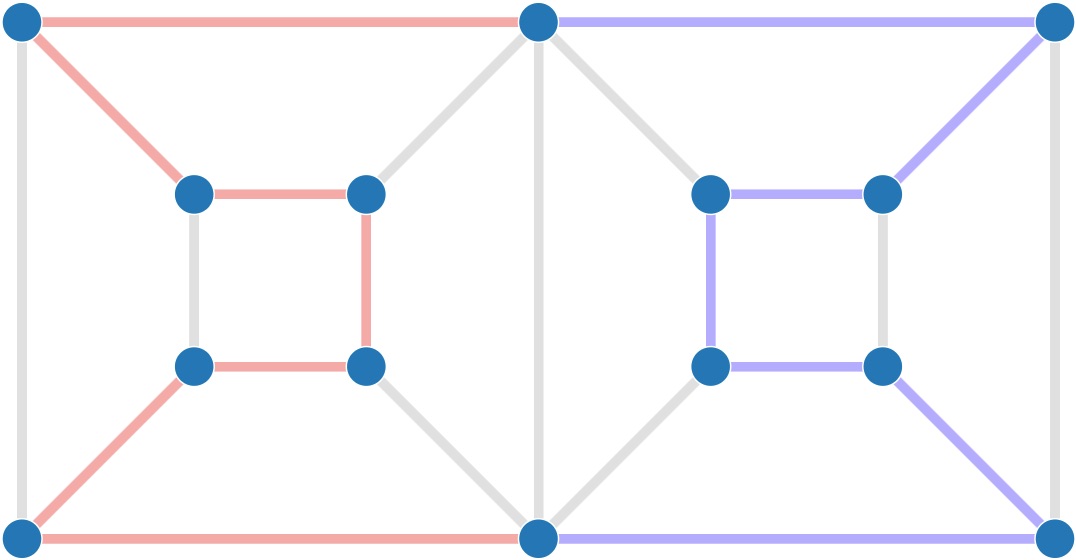
Nous avons utilisé ici une décomposition du graphe en composantes 3-sommets-connexes, ce qui se calcule très rapidement (en temps linéaire).
Les sommets de degré 2
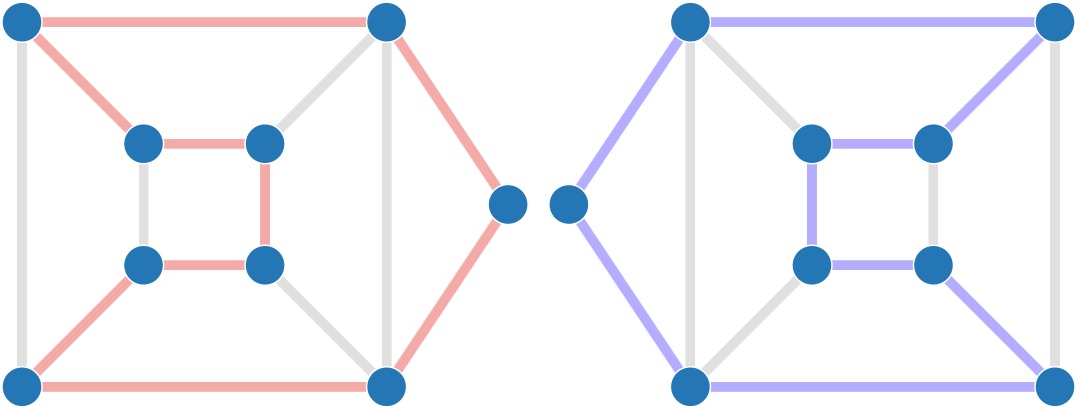
Si un sommet a degré 2, alors nous savons que ses deux arêtes incidentes sont dans le cycle. Ceci nous permet d'identifier dès le départ un ensemble d'arêtes du cycle que nous cherchons. Il est de plus important de remarquer que si le sommet u a deux voisins x et y de degré 2, alors nous pouvons éliminer du graphe toutes les autres arêtes incidentes à u. Ceci simplifie le graphe, diminue le degré d'un certain nombre de sommets, et peut ainsi révéler de nouveaux sommets de degré 2, comme le montre la figure ci-dessous.
Nous avons identifié 11 graphes pour lesquels l'application répétée de cette règle permet de résoudre le problème en réduisant le graphe à un cycle, qui n'est autre que le cycle hamiltonien recherché. Ce sont des graphes très denses, c'est à dire qu'ils ont un très grand nombre d'arêtes par rapport au nombre de sommets. Par exemple, le graphe nᵒ59 a 40001 arêtes pour 400 sommets (on ne voit pas grand chose sur la figure), et le graphe nᵒ188 a 315283 arêtes pour 1123 sommets. Ces graphes ont tous deux sommets de degré 2 qui de plus ont un voisin commun.
L'organisateur du concours nous a appris par la suite que ces graphes ont un unique cycle hamiltonien et qu'il pensait que le grand nombre d'arêtes pourrait poser problème à de nombreuses méthodes de résolution. En pratique, ces graphes n'ont posé aucun problème à notre oracle qui, en interne, procède de façon similaire en simplifiant les contraintes une à une.
Maintenant, si un sommet u a un voisin de degré 2, alors il nous reste à trouver la bonne arête parmi ses autres arêtes incidentes. Comme cette opération n'est pas simple, nous pouvons d'abord chercher à éliminer des arêtes en montrant qu'elles ne sont pas dans le cycle. Pour ce faire, nous faisons l'hypothèse qu'une arête est dans le cycle et nous interrogeons l'oracle. Si l'oracle nous répond qu'il n'existe pas de cycle hamiltonien contenant cette arête, alors nous pouvons la supprimer du graphe et passer à l'arête suivante. En procédant ainsi, nous pouvons révéler de nouveaux sommets de degré 2 et des sommets incidents à 2 sommets de degré 2, ce qui nous permet de progresser dans la résolution du problème. En règle générale, l'oracle détecte très rapidement les impossibilités. Quelques secondes suffisent. Aussi, nous avons limité le temps de calcul de l'oracle à 10 secondes et analysé sa réponse. Lorsque l'oracle répond que le problème est infaisable, nous supprimons l'arête. Si il nous retourne une solution, alors c'est que nous avons trouvé notre cycle. Enfin, si il ne sait pas décider, nous conservons l'arête et passons à la suivante (ou au sommet suivant si nous avons déjà testé toutes les arêtes). Nous avons utilisé cette technique avec succès pour les graphes 'BigDegree', comme par exemple le nᵒ268, ainsi que sur de nombreux autres graphes.
Sous-graphes isomorphes
En décomposant certains des 1001 graphes (e.g. petits motifs ou 2-connexité), nous avons obtenus des morceaux que nous avions déjà vus par ailleurs.
En effet, il se peut tout à fait que le graphe nᵒ150 soit construit en combinant le graphe nᵒ17 avec le graphe nᵒ73 ! Puisque nous avions déjà calculé un cycle hamiltonien sur ces graphes, il était plus intelligent d'essayer d'identifier les morceaux plutôt que de relancer notre oracle sur chacun d'entre eux.
La copie du graphe nᵒ17 qui pourrait se trouver à l'intérieur du graphe nᵒ150, cependant, n'est pas si facile à identifier: la raison est que le nom des sommets dans le graphe nᵒ17 n'est pas celui de leur équivalent dans le graphe nᵒ150.
Existe-t-il un programme permettant de déterminer si deux graphes dont les sommets ont des noms différents sont en réalité identiques ?
Il s'agit là du problème dit d'isomorphisme de graphe (cf. Wikipedia). A ce jour, il n'a pas été résolu de façon satisfaisante par la recherche théorique. Certains logiciels, comme Nauty, ont en pratique de très bonnes performances même si les scientifiques savent qu'il peut demander un temps exponentiel dans le pire des cas (cf. Wikipedia).
Conclusion:
Le problème du Cycle Hamiltonien est un problème NP-Complet, ce qui en fait l'un des problèmes combinatoires les plus difficiles à résoudre selon la hiérarchie de la complexité théorique. Malgré tout, il est possible d'écrire des programmes capables de résoudre des instances de grande taille (≈10 000 sommets dans le cas présent).
Suite à des discussions avec les organisateurs, il s'est avéré que l'aspect déterminant de notre approche était l'importance de la visualisation et de l'étude des propriétés des classes de graphes disponibles. Ceci a été rendu possible par l'utilisation d'une librairie JavaScript appelée d3.js, de la librairie SageMath et du solveur de programmes Linéraires CPLEX.
En effet, la plupart de nos concurrents ont abordé le concours à travers l'utilisation d'heuristiques connues pour le problème de Cycle Hamiltonien. Ces programmes effectuent leurs calculs bien plus rapidement mais ne sont pas certains de trouver la réponse: il faut donc les relancer plusieurs fois en croisant les doigts. Nous avons pour notre part opté pour une approche plus systématique d'exploration de toutes les possibilités de cycles hamiltoniens: elle est en générale plus couteuse en temps de calcul, sauf si l'on parvient à comprendre la structure des graphes et à en faire bon usage.
Ce concours nous aura donné une meilleure intuition de ce que notre Oracle était capable de résoudre de lui-même, et des différents obstacles qui le ralentissent dans ses calculs. Nous n'avons cependant pas trouvé de méthode miraculeuse qui lui permettrait de résoudre chacun des 1001 graphes sans intervention (au moins ponctuelle) d'un oeil humain.
Après tout, ce n'est que justice: il y avait également beaucoup d'intelligence dans la construction de ces 1001 graphes, et les ordinateurs ne savent jamais qu'obeir aux ordres.
Formulation du problème avec la programmation linéaire en nombres entiers
Un problème d'optimisation peut être décrit par un ensemble de variables, de contraintes sur ces variables, et d'une fonction de coût que l'on cherche à minimiser (ou maximiser) en trouvant la meilleure assignation de ses variables. Ce problème est un problème d'optimisation linéaire si ses contraintes sont des combinaisons linéaires des variables (additions et soustractions), et c'est un problème d'optimisation linéaire en nombres entiers si de plus les valeurs autorisées des variables sont entières. Nous renvoyons le lecteur à la page Wikipédia sur l'optimisation linéaire en nombres entiers pour plus de détails sur cette technique.
Comment écrire le problème du cycle hamiltonien comme un problème d'optimisation linéaire en nombres entiers ? Tout d'abord, nous cherchons un sous-ensemble d'arêtes du graphe $G=(V,E)$, où $V$ est l'ensemble des $n$ sommets et $E$ est l'ensemble des arêtes. Il est donc naturel d'utiliser une variable $x_e$ pour chaque arête $e$ qui prendra la valeur 1 si l'arête est sélectionnée et 0 sinon. $$x_e = \begin{cases} 1 & \text{si l'arête est sélectionnée}\\ 0&\text{sinon}\end{cases}$$ Ensuite, l'ensemble d'arêtes que nous cherchons doit former un cycle passant une et une seule fois par chaque sommet. Dans un cycle, chaque sommet est incident à 2 arêtes sélectionnées. Notre première contrainte est donc que la somme des variables $x_e$ correspondants aux arêtes $e$ incidentes à un sommet $u$ soit égale à 2. $$\sum_{e=(u,v),\ v\text{ voisin de }u}x_e = 2$$ Cette contrainte nous garantit également que nous allons sélectionner le bon nombre d'arêtes, mais elle n'est pas suffisante pour assurer que ces arêtes forment un unique cycle et pas plusieurs cycles disjoints. Nous avons donc besoin de contraintes assurant la connexité de l'ensemble des arêtes sélectionnées.
Il existe plusieurs façons d'exprimer la contrainte de connexité en programmation linéaire. Nous en avons choisi une basée sur les coupes du graphe. Tout d'abord, rappelons qu'une coupe arêtes du graphe est l'ensemble $C$ des arêtes entre les sommets d'un sous-ensemble $A$ de sommets du graphe et les autres sommets ($B = V\setminus A$) du graphe. Si nous retirons du graphe les arêtes de l'ensemble $C$, alors il ne sera plus possible de trouver un chemin entre un sommet $u$ de $A$ et un chemin $v$ de $B$. C'est exactement comme ce que nous avons vu dans la section 2-connexité.
Une propriété essentielle ici est qu'un cycle hamiltonien doit traverser au moins deux fois chaque coupe du graphe, autant de fois pour aller de $A$ vers $B$ que pour revenir de $B$ vers $A$. Dans le cas contraire, il ne serait pas possible d'obtenir un cycle. Ceci se traduit par la contrainte suivante qui exprime que la somme des variables correspondants aux arêtes de la coupe $C$ doit être supérieure ou égale à 2: $$\sum_{e\in C} x_e \geq 2$$
L'utilisation de cette contrainte pose tout de même une difficulté importante: nous avons besoin d'une contrainte par coupe du graphe, or il y a un nombre exponentiel ($2^n$) de coupes dans le graphe. C'est beaucoup trop pour nos ordinateurs. Heureusement, en pratique, nous pouvons introduire ces contraintes au fur et à mesure, en ajoutant à chaque itération les meilleures contraintes possible pour progresser dans la résolution du problème. L'idée est que de nombreuses coupes ne sont pas utiles pour trouver la solution et qu'il est certainement possible de réduire considérablement le nombre de contraintes à ajouter. C'est la technique de la génération de contraintes, ou décomposition de Benders. Plus précisemment, nous résolvons le problème avec un premier ensemble de contraintes (celles sur le degré par exemple). Si l'ensemble des arêtes sélectionnées est connexe alors nous avons gagné, et nous pouvons retourner le cycle hamiltonien. Sinon, nous construisons le graphe $H$ des arêtes sélectionnées et nous identifions ses composantes connexes. Remarquons ici que chaque composante connexe $A$ du graphe $H$ définit une coupe arête dans le graphe $G$. Il suffit de prendre l'ensemble $C$ des arêtes reliant les sommets de $A$ aux autres sommets du graphe $G$. Nous ajoutons alors dans le programme une contrainte pour chaque coupe $C$ ainsi définie, puis nous résolvons à nouveau.
Cette méthode est assez performante en pratique et nous l'avons utilisé pour notre oracle. Par exemple, la solution du graphe n°1000 a été obtenue avec l'ajout de seulement 3200 contraintes de coupes sur les $2^{9058}$ possibles. Ceci montre bien que l'ensemble des coupes vraiment utiles est très petit par rapport à la taille de l'ensemble des coupes possibles qui est lui gigantesque ($2^{9058}\simeq 5.3\ 10^{2725})$. Par contre, comme le montre les exemples de temps de calculs que nous avons présenté plus haut, cette méthode n'est pas adaptée aux graphes comme le n°12.